What is a confusion matrix in machine learning?
A confusion matrix is an evaluation tool for a machine learning classification model. It sums up the performance of a classifier in a visual way and from it, we can derive other metrics such as accuracy, precision and recall.
There are several types of machine learning classification problems:
- Binary classification
- Multi-class classification
- Multi-label classification
What we can extract directly from a confusion matrix
To explore the value in a confusion matrix, let’s use a binary classification problem.
A machine learning classifier, applied to a binary classification problem, has to make predictions (True or False), and therefore can output 4 types of outcomes:
-
True positive (TP) where the truth label and the model’s prediction are both true (so the model has made a correct prediction)
-
True negative (TN) where the truth label and the model’s prediction are both false (so the model has also made a correct prediction)
-
False positive (FP) where the truth label is false but the model’s prediction is true (so the model is wrong)
-
False negative (FN) where the truth label is true but the model’s prediction is false (so the model is also wrong).
A confusion matrix groups these four outcomes to give us an overview of the model’s performance.
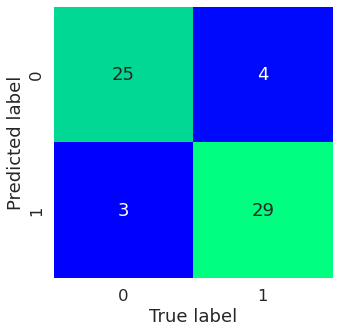
In the above matrix, there are:
- 29 true positives
- 25 true negatives
- 3 false positives
- 4 false negatives
Because it’s visual, it’s rather easy to infer whether or not the model is performing well or poorly. As you can see, the true positives and negatives are located on the identity diagonal of the matrix.
What can we deduce from a confusion matrix
From this matrix, we can derive other important metrics:
- Accuracy
- Precision
- Recall
Accuracy
Accuracy determines the overall performance of the model, which is out of all the predictions that it made, how many were correct? It can be summed up into this equation: \(Accuracy = \frac{TP+TN}{TP+FP+TN+FN}\)
Precision
Precision can be thought of this way: out of all positive predictions, how many were correct? And its related equation is: \(Precision = \frac{TP}{TP+FP}\)
Recall
Recall can be thought of this way: out of all positive labels, how many were correctly predicted? Its related equation is: \(Recall = \frac{TP}{TP+FN}\)
The remaining challenge relies in the evaluation criterion, which of these metrics should you favor?
It greatly depends on your project’s success criterion.